
Grille de sudoku classique

Variante du sudoku basée sur des comparaisons entre les cases
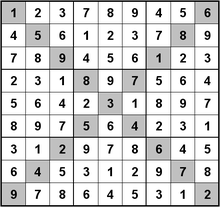
Sudoku classique avec une contrainte supplémentaire sur les diagonales
Le jeu du sudoku consiste à compléter une grille carrée divisée en N régions de N cases, en partie remplie avec des chiffres, de façon que dans chaque ligne, chaque colonne et chaque région les chiffres de 1 à N apparaissent une et une seule fois.
Une analyse mathématique du sudoku permet de découvrir les différentes propriétés et problèmes qui se cachent derrière ce jeu et ses variantes.
L'analyse mathématique du sudoku se divise en deux grandes parties : l'analyse des propriétés des grilles complètes et l'analyse de la résolution d'une grille.
L'analyse des grilles s'est en grande partie focalisée sur l'énumération des solutions possibles pour différentes variantes du jeu. L'étude de la résolution se concentre sur les valeurs initiales de la grille et sur les étapes qui mènent à la grille complète. Ces techniques font appel à plusieurs disciplines : analyse combinatoire, algorithmique, théorie des groupes ainsi que la programmation puisque l'ordinateur permet de rapidement résoudre les grilles.
Il y a un grand nombre de variantes du sudoku, en général caractérisées par la taille de la grille (le paramètre N) et la forme des régions. Les sudokus classiques ont un N égal à 9 avec des régions de 3 × 3 cases. Un sudoku rectangulaire possède des régions rectangulaires d'une taille L × C où L est le nombre de lignes et C le nombre de colonnes. Un tel sudoku, avec une taille de L × 1 (ou 1 × C), devient un carré latin puisque la région est une ligne ou une colonne unique.
Des variantes plus complexes existent comme celles avec des régions découpées de manière irrégulière (Nanpure), avec des contraintes supplémentaires (Samunamupure ou Killer Sudoku, respect de l'unicité sur les diagonales avec le Kokonotsu, contraintes sur l'ordre des éléments avec le Greater-Than) ou des assemblages de plusieurs grilles (Samurai, Sudoku en 3D). Dans certaines variantes, les chiffres sont remplacés par des lettres. Cette substitution des caractères utilisés ne change toutefois rien aux propriétés intrinsèques du puzzle si les règles restent les mêmes.
L'analyse mathématique du sudoku a suivi la popularité du jeu. Les analyses concernant la complexité algorithmique et le caractère NP-complet du jeu furent documentés vers la fin de l'année 20021, les résultats d'énumération ont fait leur apparition vers le milieu de l'année 20052. Les contributions des nombreux chercheurs et amateurs ont permis de mettre à jour les propriétés du jeu. L'apparition des variantes du sudoku étend d'autant plus les éléments mathématiques à considérer et explorer.
Contrastant avec les deux approches mathématiques principales citées au début, une approche basée sur la logique mathématique et s'attaquant au problème de la résolution des puzzles a été proposée récemment dans le livre de Denis Berthier, « The Hidden Logic of Sudoku »3 (La logique cachée du sudoku). Cela a permis de découvrir et de formaliser toutes les symétries généralisées du jeu et de découvrir de nouvelles règles de résolution basées dessus, comme les chaînes xy cachées.
Le problème de placer des chiffres sur une grille de n2 × n2 comprenant n × n régions est prouvé NP-complet4.
La résolution d'un sudoku peut être formalisée par le problème de la coloration de graphe. Le but, dans la version classique du jeu, est d'appliquer 9 couleurs sur un graphe donné, à partir d'un coloriage partiel (la configuration initiale de la grille). Ce graphe possède 81 sommets, un par cellule. Chacune des cases du sudoku peut être étiquetée avec un couple ordonné (x, y), où x et y sont des entiers compris entre 1 et 9. Deux sommets distincts étiquetés par (x, y) et (x’, y’) sont reliés par une arête si et seulement si :
- x = x’ (les deux cellules appartiennent à la même ligne) ou,
- y = y’ (les deux cellules appartiennent à la même colonne) ou,
- {\displaystyle \left\lceil {\dfrac {x}{3}}\right\rceil =\left\lceil {\dfrac {x'}{3}}\right\rceil }
 et {\displaystyle \left\lceil {\dfrac {y}{3}}\right\rceil =\left\lceil {\dfrac {y'}{3}}\right\rceil }
et {\displaystyle \left\lceil {\dfrac {y}{3}}\right\rceil =\left\lceil {\dfrac {y'}{3}}\right\rceil } (les deux cellules appartiennent à la même région).
(les deux cellules appartiennent à la même région).
La grille se complète en affectant un entier entre 1 et 9 pour chaque sommet, de façon que tous les sommets liés par une arête ne partagent pas le même entier.
Une grille solution est aussi un carré latin. La relation entre les deux théories est désormais complètement connue, depuis que D. Berthier a démontré, dans « The Hidden Logic of Sudoku »3, qu'une formule logique du premier ordre qui ne mentionne pas les blocs (ou régions) est valide pour le sudoku si et seulement si elle est valide pour les carrés latins.
Il y a notablement moins de grilles solutions que de carrés latins, car le sudoku impose des contraintes supplémentaires (Voir ci-dessous point 4 : nombre de grilles complètes possibles).
Contrairement au nombre de grilles solutions, le nombre exact de puzzles minimaux n'est pas connu. (Un puzzle est minimal si aucun dévoilé ne peut être supprimé sans compromettre l'unicité de la solution.) Cependant, des techniques statistiques combinées avec la définition d'un nouveau type de générateur (générateur à biais contrôlé5(en)) permettent de montrer qu'il y a approximativement (avec une erreur relative de 0.065%) :
- 3,10 × 1037 puzzles minimaux,
- 2,55 × 1025 puzzles minimaux non équivalents.
(voir le livre Pattern-Based Constraint Satisfaction and Logic Puzzles6 ou l'article Unbiased Statistics of a CSP - A Controlled-Bias Generator7).
Le nombre maximum de dévoilés sans qu'une solution unique n'apparaisse immédiatement, peu importe la variante, est la taille de la grille moins 4 : si deux paires de candidats ne sont pas inscrits et que les cellules vides occupent les coins d'un rectangle, et qu'exactement deux cellules sont dans une région, alors il existe deux façons d'inscrire les candidats. L'opposé de ce problème, à savoir le nombre minimum de dévoilés pour garantir une solution unique, est un problème non résolu, bien que des enthousiastes japonais aient découvert une grille 9 × 9 sans symétrie qui contient seulement 17 dévoilés (pour en savoir plus, voir (en)). Un résultat8 publié en 2007, dévoile que pour qu'un sudoku ait une solution unique, il est nécessaire que 8 des 9 chiffres soient dévoilés9,10, alors que 18 est le nombre minimum de dévoilés pour les grilles 9 × 9 symétriques.
Un puzzle est une grille incomplète où figurent des valeurs initiales. Les régions sont également appelées des blocs ou des zones. Le terme de carré est évité pour lever toute confusion.
Une bande est une suite de blocs adjacents sur l'axe horizontal. Une pile est une suite de blocs adjacents sur l'axe vertical. Dans un sudoku de 9 × 9 cases, il y a ainsi 3 bandes et 3 piles.
Un sudoku correctement conçu a une et une seule solution : la grille finale est unique, mais la résolution à partir de la grille partielle peut toutefois prendre des chemins différents.
Le nombre de grilles complètes possibles est de 9! × 722 × 27 × 27 704 267 971 (soit 6 670 903 752 021 072 936 960 grilles ≈ 6,67 × 102111,12,13).
Le dernier facteur est un nombre premier. Ce résultat a été prouvé en 2005 par Bertram Felgenhauer et Frazer Jarvis14 grâce à une recherche exhaustive. Frazer Jarvis a ensuite considérablement simplifié la preuve grâce à une analyse détaillée. La démonstration a été validée de manière indépendante par Ed Russell.
Cependant, plusieurs grilles sont équivalentes si on prend en compte un certain nombre de symétries, à savoir
- permutations des 9 nombres
- échange des lignes avec les colonnes (transposition)
- permutation des lignes dans une bande (en ligne)
- permutation des colonnes dans une pile (en colonne)
- permutation des bandes en ligne
- permutation des piles en colonne
(On remarque l'analogie avec les opérations matricielles en algèbre linéaire). En tenant compte de ces symétries, Jarvis et Russell ont montré qu'il y avait 5 472 730 538 grilles non équivalentes15,13.
À l'inverse, à cette date, aucun résultat n'existe sur le nombre de grilles complètes dans un super sudoku (grille 16 × 16).
Si maintenant, on s'intéresse aux nombres de problèmes proposables, ce nombre est nettement plus important car il existe plusieurs façons de révéler les chiffres d'une même grille.
Le minimum de cases remplies au préalable pour rendre la résolution unique est de 17; il a été prouvé par le calcul en par une équipe irlandaise16,13. Une liste de l'ensemble des sudokus à solution unique ayant 17 cases remplies a été établie par des japonais9 ,17.
La réponse à la question « Combien y a-t-il de sudokus ? » dépend de la définition d'une solution et de l'équivalence entre plusieurs solutions. Pour l'énumération de toutes les solutions possibles (c.-à-d. grilles complètes), on retient la définition suivante :
Une grille A est différente d'une grille B, si la valeur de la case en A(i, j) est différente de B(i, j), pour au moins un couple i, j (valeurs limitées par la dimension de la grille).
Si une grille A est obtenue par symétrie de la grille B alors elles sont considérées comme différentes. Les rotations sont également comptées comme de nouvelles solutions.
Notation avec les régions, les triplets h56 et v56
|
|
|
|
|
|
|
|
|
|
|
|
Soit :
- s une solution d'un sudoku avec des dimensions spécifiques et qui satisfait les règles du sudoku original (pas de doublons dans les lignes, colonnes et régions)
- S = {s}, l'ensemble de toutes les solutions possibles
- |S|, la cardinalité (taille) de l'ensemble S (c.-à-d. le nombre de solutions)
Le nombre de solutions dépend de la taille de la grille, des règles appliquées et de la définition précise d'une solution distincte. Pour un sudoku avec des régions de 3 × 3, les conventions pour l'affichage du contenu de la grille sont les suivantes : les bandes sont numérotées du haut vers le bas, les piles de la gauche vers la droite. Les régions sont donc numérotées de la gauche vers la droite et du haut vers le bas. Cette convention s'applique aussi pour les grilles rectangulaires.
D'autres termes sont utiles dans le cas du sudoku avec des régions de 3 × 3 :
- le triplet est une combinaison non-ordonnée de trois valeurs présentes sur une ligne ou une colonne d'une région. Par exemple, le triplet {3, 5, 7} signifie que les valeurs 3, 5, 7 apparaissent dans une ligne ou une colonne de la région, mais sans spécifier leur ordre d'apparition (on pourrait avoir une ligne avec 5, 7, 3 ou encore une colonne avec 3, 7, 5). Les valeurs d'un triplet peuvent être arrangées de 6 manières différentes (3!) grâce à des permutations. Par convention, les éléments d'un triplet sont écrits dans l'ordre croissant mais cela ne signifie pas qu'ils apparaissent dans la grille selon le même ordre ;
- la notation hRL indique un triplet pour la région R et la ligne L de la grille. Le préfixe h indique qu'il s'agit d'un triplet horizontal ;
- de manière similaire, la notation vRC identifie un triplet pour la région R et la colonne C de la grille. Le préfixe v indique qu'il s'agit d'un triplet vertical.
Par exemple, la notation h56 correspond au triplet de la région 5, ligne 6. En anglais, on utilise la notation r pour row et c pour column.
On parle aussi de mini-ligne ou de mini-colonne pour désigner la portion présente dans une région d'une ligne ou d'une colonne de la grille.
Énumérations des solutions symétriquement distinctes[modifier | modifier le code]
Deux grilles sont dites symétriquement distinctes si l'une ne peut être dérivée de l'autre (par une ou plusieurs opérations de préservation de la symétrie).
Les opérations suivantes transforment toujours une grille valide en une autre grille valide :
- changer le label de chaque symbole (9!)
- permutations des bandes (3!)
- permutations des piles (3!)
- permutations des lignes dans une bande (3!3)
- permutations des colonnes dans une pile (3!3)
- réflexion, transposition, rotation de 90° (avec l'une de ces opérations et les permutations, il est possible de déduire les autres opérations, ce qui fait que ces opérations ne contribuent qu'avec un facteur de 2).
Ces opérations définissent une relation de symétrie entre deux grilles équivalentes. En excluant le changement de labels, et en considérant les 81 valeurs présentes dans la grille, ces opérations forment un sous-groupe du groupe symétrique S81 avec un ordre 3!8 × 2 = 3 359 232.
Identifier les solutions grâce au lemme de Burnside[modifier | modifier le code]
Pour une solution, l'ensemble des solutions équivalentes qui peut être obtenu en utilisant ces opérations (sauf le renommage des valeurs), forme une orbite du groupe symétrique. Le nombre de solutions symétriquement distinctes est ainsi le nombre d'orbites, une valeur qui peut être calculée grâce au lemme de Burnside. Les points fixes de la méthode de Burnside sont des solutions qui ne diffèrent que par le renommage. Grâce à cette technique, Jarvis Russell a calculé le nombre de solutions symétriquement distinctes : 5 472 730 538.
Pour des grandes valeurs de L et C, la méthode de Kevin Kilfoil18 (généralisée par la suite19) est utilisée pour estimer le nombre de façons de compléter une grille. Cette méthode part du principe que les contraintes sur les lignes et les colonnes sont, pour une première approximation, des variables aléatoires conditionnellement indépendantes eu égard à la contrainte sur la région. Des calculs algébriques permettent d'aboutir à la formule de Kilfoil-Silver-Pettersen :
- {\displaystyle {\mbox{Nombre de grilles}}\simeq {\dfrac {b_{L,C}^{C}\times b_{C,L}^{L}}{(LC)!^{LC}}}}

où bL, C est le nombre de manières de compléter un sudoku avec L régions (d'une taille de L × C) horizontalement adjacentes. L'algorithme de Pettersen20, implémenté par Silver21 est actuellement la technique la plus rapide connue pour évaluer de manière exacte les valeurs bL, C.
Le compte des bandes pour les problèmes dont « le nombre total de grilles de sudoku est inconnu » est donné ci-dessous. Comme dans le reste de cet article, les dimensions correspondent à celles des régions.
-
| Dimensions | Nombre de bandes | Auteur(s) | Vérification formelle |
|---|
| 2 × C |
(2C)! (C!)2 |
(évident) |
Oui |
| 3 × C |
{\displaystyle (3C)!(C!)^{6}\sum _{k=0\ldots C}{C \choose k}^{3}} |
Pettersen [archive] |
Oui |
| 4 × C |
(Voir ci-dessous pour le résultat mathématique.) |
Pettersen [archive] |
Oui [archive] |
| 4 × 4 |
16! × 4!12 × 1 273 431 960 = c. 9.7304 × 1038 |
Silver [archive] |
Oui |
| 4 × 5 |
20! × 5!12 × 879 491 145 024 = c. 1.9078 × 1055 |
Russell [archive] |
Oui |
| 4 × 6 |
24! × 6!12 × 677 542 845 061 056 = c. 8.1589 × 1072 |
Russell [archive] |
Oui |
| 4 × 7 |
28! × 7!12 × 563 690 747 238 465 024 = c. 4.6169 × 1091 |
Russell [archive] |
Oui |
| (Des calculs jusqu'à 4 × 100 ont été effectués par Silver [archive], mais ne sont pas indiqués ici.) |
| 5 × 3 |
15! × 3!20 × 324 408 987 992 064 = c. 1.5510 × 1042 |
Silver [archive] |
Oui# |
| 5 × 4 |
20! × 4!20 × 518 910 423 730 214 314 176 = c. 5.0751 × 1066 |
Silver [archive] |
Oui# |
| 5 × 5 |
25! × 5!20 × 1 165 037 550 432 885 119 709 241 344 = c. 6.9280 × 1093 |
Pettersen/Silver [archive] |
Non |
| 5 × 6 |
30! × 6!20 × 3 261 734 691 836 217 181 002 772 823 310 336 = c. 1.2127 × 10123 |
Pettersen/Silver [archive] |
Non |
| 5 × 7 |
35! × 7!20 × 10 664 509 989 209 199 533 282 539 525 535 793 414 144 = c. 1.2325 × 10154 |
Pettersen/Silver [archive] |
Non |
| 5 × 8 |
40! × 8!20 × 39 119 289 737 902 332 276 642 894 251 428 026 550 280 700 096 = c. 4.1157 × 10186 |
Pettersen/Silver [archive] |
Non |
- # : même auteur mais avec une autre méthode
L'expression pour le cas 4 × C est : {\displaystyle (4C)!(C!)^{12}\sum _{a,b,c}{\left({\dfrac {C!^{2}}{a!b!c!}}\times \sum _{\begin{matrix}k_{12},k_{13},k_{14},\\k_{23},k_{24},k_{34}\end{matrix}}{{a \choose k_{12}}{b \choose k_{13}}{c \choose k_{14}}{c \choose k_{23}}{b \choose k_{24}}{a \choose k_{34}}}\right)^{2}}}
avec :
- la somme extérieure s'applique sur tous les a, b, c tel que 0 ⩽ a, b, c et a+b+c=2C
- la somme intérieure s'applique sur tous les k12,k13,k14,k23,k24,k34 = 0 tel que
- k12,k34 = a et
- k13,k24 = b et
- k14,k23 = c et
- k12+k13+k14 = a-k12+k23+k24 = b-k13+c-k23+k34 = c-k14+b-k24+a-k34 = C
Plusieurs types de contraintes existent sur des sudokus avec des régions de 3 × 3. Les noms n'ayant pas été standardisés, les liens externes pointent vers les définitions :
Tous les sudokus sont valides (unicité des nombres dans les lignes, colonnes et régions) après l'application des opérations qui préservent les propriétés du groupe du sudoku. Certains sudokus sont spéciaux dans le sens où certaines opérations ont le même effet que le renommage des chiffres :
| Transformation | Nombre de grilles | Auteur(s) | Vérification formelle |
|---|
| Transposition |
10 980 179 804 160 |
Russell [archive] |
Indirectement |
| Quart de tour |
4 737 761 280 |
Indirectement |
| Moitié de tour |
56 425 064 693 760 |
Indirectement |
| Permutation des bandes |
5 384 326 348 800 |
Indirectement |
| Permutations des lignes dans les bandes |
39 007 939 461 120 |
Indirectement |
Les grilles correctement réalisées doivent avoir une et une seule solution. Une grille est dite irréductible ou minimale si elle est valide et si le retrait d'un chiffre supplémentaire entraîne son invalidité (c.-à-d. elle n'admet plus de solution unique). Il est possible de créer des grilles minimales avec un nombre différent de valeurs initiales. Cette section décrit les propriétés relatives à ce problème.
Le sudoku classique avec une grille de 9 × 9, soit 81 cases, est pour l'instant limité par une borne inférieure de 17 valeurs initiales, ou 18 quand les positions des chiffres initiaux peuvent être tournées de 90°. Il existe une conjecture qui stipule que cette borne de 17 est la meilleure possible, mais il n'existe pas de preuve formelle, seulement une recherche exhaustive avec des grilles aléatoires :
- Gordon Royle a compilé une liste de grilles avec 17 valeurs22, lesquelles sont uniques. Parmi ces 39 422 grilles, aucune d'entre elles n'est isomorphe à une autre grille ou contient une solution avec 16 valeurs initiales.
- Une construction indépendante de 700 grilles distinctes a permis de découvrir 33 autres grilles qui n'apparaissaient pas dans la liste de Royle. Une estimation d'après le maximum de vraisemblance, permet de déduire que le nombre de ces grilles minimales s'élève à environ 34 550. Si les méthodes sont vraiment aléatoires et indépendantes, alors la probabilité de trouver une construction valide avec 16 valeurs initiales est faible. En effet, une seule de ces hypothétiques grilles permettrait d'obtenir 65 nouvelles grilles avec 17 valeurs initiales, résultats qui ne sont pas apparus dans les recherches précédentes. Mais en l'absence d'une preuve formelle, ce fait ne peut être confirmé ou infirmé.
- D'autres recherches aléatoires ont fourni des grilles qui étaient déjà dans la liste de Royle23,24, ce qui renforce l'idée de la quasi-complétude de l'ensemble fourni par Royle.
Des contraintes supplémentaires (avec des sudokus dont les régions font 3 × 3) changent le nombre de valeurs minimales nécessaires pour aboutir à une solution unique :
- 3doku : aucun résultat connu à ce jour (2006).
- Groupes disjoints25, des grilles avec 12 valeurs ont été démontrées par Glenn Fowler. Rien n'indique que cette borne minimale ne peut être réduite.
- Hypercube26, des grilles avec 8 valeurs ont été proposées par Guenter Stertenbrink.
- Magic Sudoku27, un exemple avec 7 valeurs a été publié par Guenter Stertenbrink. Ici encore, on ne sait pas s'il s'agit véritablement de la borne minimale.
- Sudoku X28, Gordon Royle a donné un exemple avec 17 valeurs, borne supposée minimale.
- NRC Sudoku29, Andries Brouwer a découvert un exemple avec 11 valeurs. On ne sait pas s'il est possible de faire mieux.
Une région peut être décrite par ses dimensions : L × C où L est le nombre de lignes et C le nombre de colonnes dans la région. Dans la version classique du sudoku, L = C = 3. Cela implique qu'il existe L régions par bande et C régions par pile. Il est plus pratique de mentionner la taille de la région plutôt que le nombre d'éléments car une région de 2 × 6 a le même nombre de cases que celle de 3 × 4.
La découpe suivante peut être adoptée pour classifier grossièrement les variantes :
- régions rectangulaires
- régions irrégulières (polyomino)
Des contraintes supplémentaires permettent de mieux cibler le type de jeu.
Un sudoku carré de N × N régions possède plusieurs propriétés respectées pour tous ses sous-éléments, en plus de la règle classique de l'absence de doublons. En effet, chaque ligne et chaque colonne a une intersection avec N régions et partage N cases avec chacune d'entre elles. Le nombre de bandes et de piles est aussi égal à N. Le sudoku rectangulaire n'a pas ces propriétés.
Le sudoku avec des régions de 3 × 3 cache une autre propriété qui lui est propre : N est le nombre de sous-unités considérées dans le jeu, à savoir trois : la ligne, la colonne et la région.
Les Du-sum-oh30 remplacent les régions de 3 × 3 (ou plus généralement L × C) par des régions irrégulières avec une taille fixe. Bob Harris a prouvé qu'il était toujours possible de créer des du-sum-ohs avec N-1 valeurs initiales sur une grille de N par N31. Il a donné plusieurs exemples.
Dans le Samunamupure ou Killer Sudoku, les régions ont non seulement des formes irrégulières mais également des tailles différentes. Les règles d'unicité des nombres dans les lignes, régions et colonnes s'appliquent toujours. Les indications initiales sont données sous la forme de sommes de valeurs dans les régions (par exemple, une région de 4 cellules avec une somme de 10 contiendra les chiffres 1, 2, 3, 4 selon un certain ordre). Le nombre minimal de valeurs nécessaires pour commencer la grille n'est pas connue, ni conjecturée.
Une variante proposée par Miyuki Misawa32 remplace les sommes par des relations : les indications sont des symboles =, <, >, montrant les valeurs relatives pour certaines régions adjacentes. Un exemple avec seulement 8 relations est donné, mais on ne sait pas si ce nombre est la borne inférieure.
Méthode de Felgenhauer/Jarvis pour l'énumération de la grille de 9 × 9[modifier | modifier le code]
L'approche décrite ici est historiquement la première stratégie employée pour énumérer les solutions d'une grille de sudoku classique (régions de 3 × 3 dans une grille de 9 × 9). Elle a été proposée par Felgenhauer et Jarvis2.
L'analyse débute par l'étude des permutations de la première bande utilisée dans des solutions valides. Une fois que la classe d'équivalence et les symétries de cette bande, pour des solutions partielles, sont identifiées, on s'intéresse aux deux autres bandes qui sont construites et comptées pour chaque classe d'équivalence. En effectuant la somme de l'ensemble des combinaisons, on obtient le nombre total de solutions, soit 6 670 903 752 021 072 936 960 (environ 6,67 × 1021).
Afin de réduire l'espace de recherche, on part du principe que le renommage (par exemple changer le « 1 » en « 2 » et vice-versa) des cases produit une solution équivalente. Une grille autorise 9! = 362 880 renommages de ce type : un chiffre choisi parmi les 9 chiffres possibles est attribué au premier type de case, un chiffre parmi les 8 restants est attribué au deuxième type de case, un chiffre parmi les 7 restants est attribué au troisième type de case, etc.
- ↑ « (lien) » (sur l'Internet Archive)
- ↑ Revenir plus haut en :a et b http://www.afjarvis.staff.shef.ac.uk/sudoku/sudoku.pdf [archive]
- ↑ Revenir plus haut en :a et b (en) Denis Berthier, « The Hidden Logic of Sudoku », Lulu Publishers, (lire en ligne [archive])
- ↑ pour plus de détails, voir (en) [1] [archive]
- ↑ https://github.com/denis-berthier/Controlled-bias_Sudoku_generator_and_collection [archive]
- ↑ (en) Denis Berthier, « Pattern-Based Constraint Satisfaction and Logic Puzzles », Lulu Publishers, (ISBN 978-1-291-20339-4),
- ↑ Denis Berthier, Unbiased Statistics of a CSP - A Controlled-Bias Generator, International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 09), December 4-12, 2009
- ↑ Solving Sudokus---Coloring by Numbers [archive]
- ↑ Revenir plus haut en :a et b http://www2.ic-net.or.jp/~takaken/auto/guest/bbs46.html [archive]
- ↑ (en) http://www.csse.uwa.edu.au/~gordon/sudokumin.php [archive]]
- ↑ (en) http://www.shef.ac.uk/~pm1afj/sudoku/ [archive]
- ↑ suite A107739 de l'OEIS
- ↑ Revenir plus haut en :a b et c Jean-Paul Delahaye, Le problème du sudoku, Pour la Science no 447, janvier 2015, p. 76-81
- ↑ http://www.shef.ac.uk/~pm1afj/sudoku/ [archive]
- ↑ http://www.shef.ac.uk/~pm1afj/sudoku/sudgroup.html [archive] (pour plus de détails, voir (en)http://www.shef.ac.uk/~pm1afj/sudoku/sudgroup.html [archive] et suite A109741 de l'OEIS)
- ↑ https://arxiv.org/pdf/1201.0749v1.pdf [archive]
- ↑ http://www.csse.uwa.edu.au/~gordon/sudokumin.php [archive]
- ↑ Sudoku Players' Forums :: View topic - Su-Doku's maths [archive]
- ↑ Sudoku Players' Forums :: View topic - Su-Doku's maths [archive]
- ↑ Sudoku Players' Forums :: View topic - RxC Sudoku band counting algorithm [archive]
- ↑ Sudoku Players' Forums :: View topic - RxC Sudoku band counting algorithm [archive]
- ↑ Minimum Sudoku [archive]
- ↑ Gary McGuire's Minimum Sudoku Page, Sudoku Checker [archive]
- ↑ http://www.csse.uwa.edu.au/~gordon/sudokupat.php?cn=3 [archive]strangely familiar
- ↑ Sudoku Players' Forums :: View topic - Minimum number of clues in Sudoku DG [archive]
- ↑ http://magictour.free.fr/sudoku6 [archive]
- ↑ Sudoku Players' Forums :: View topic - Number of « magic sudokus » (and random generation) [archive]
- ↑ Sudoku Players' Forums :: View topic - 13-clue Sudoku X [archive]
- ↑ NRC Sudokus [archive]
- ↑ × 9/index.html Du-Sum-Oh Puzzles [archive]
- ↑ Du-Sum-Oh Puzzles [archive]
- ↑ Sum Number Place( =, < > ) [archive]